my photos

Maths Poem

A MATH POEM ON FRIENDSHIP

0% INVEST AND 100% INTEREST

Friendship is infinity,
containing only plus points.
So, my friend you are a Modulus.
If the world is a circle,
You are a point on the circumference,
I am a tangent,
which will touch the circle at that point.
If I am a straight lineYou are a lso the same my friend.
For we are not perpendicular,
but always coincide.

Trigonometry

Applications of Trigonometry in Real life

• Trigonometry is commonly used in finding the height of towers and mountains.

• It is used in navigation to find the distance of the shore from a point in the sea.

• It is used in oceanography in calculating the height of tides in oceans

• It is used in finding the distance between celestial bodies

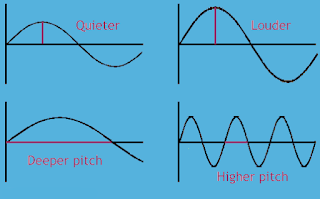
• The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.

• Architects use trigonometry  to calculate structural load, roof slopes, ground surfaces and many other aspects, including sun shading and light angles

Application

Introduction:

•  The Laplace transform is named in honor of mathematician and astronomer Pierre-Simon Laplace, who used the transform in his work on probability theory.

• Like the Fourier transform, the Laplace transform is used for solving differential and integral equations.

• Laplace transform is a widely used integral transform.

• Laplace transform is just a shortcut for complex calculations.

 Real Life Applications:

•    The Laplace transform turns a complicated nth order differential equation to a corresponding nth degree polynomial.
  
  
• In physics and engineering, it is used for analysis of linear time-invariant systems such as electrical circuits, harmonic oscillators, optical devices, and mechanical systems.

• The Laplace transform is one of the most important equations in digital signal processing and electronics.

•  In Nuclear physics, Laplace transform is used to get the correct form for radioactive decay.

• It has also been applied to the economic and managerial problems, and most recently, to Materials Requirement Planning (MRP) 

• The Laplace transform reduces a linear differential equation to an algebraic equation, which can then be solved by the formal rules of algebra

maths in nature

MATHS AND NATURE

"The laws of nature are but the mathematical thoughts of God"

                                                                                      - Euclid

Mathematics is everywhere in this universe. We seldom note it. We enjoy nature and are not interested in going deep about what mathematical idea is in it. Here are a very few properties of mathematics that are depicted  in nature.

SYMMETRY

Symmetry is everywhere you look in nature .

Symmetry is when a figure has two sides that are mirror images of one another. It would then be possible to draw a line through a picture of the object and along either side the image would look exactly the same. This line would be called a line of symmetry.

There are two kinds of symmetry.

One is bilateral symmetry in which an object has two sides that are mirror images of each other.

The human body would be an excellent example of a living being that has bilateral symmetry.




Few more pictures in nature showing bilateral symmetry.

The other kind of symmetry is radial symmetry. This is where there is a center point and numerous lines of symmetry could be drawn.

The most obvious geometric example would be a circle.



Few more pictures in nature showing radial symmetry.

SHAPES

Geometry is the branch of mathematics  that describes shapes.

Sphere:

A sphere  is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball.

The shape of the Earth is very close to that of an oblate spheroid, a sphere flattened along the axis from pole to pole such that there is a bulge around the equator.

Hexagons:

Hexagons are six-sided polygons, closed, 2-dimensional, many-sided figures with straight edges.

 
For a beehive, close packing is important to maximise the use of space. Hexagons fit most closely together without any gaps; so hexagonal wax cells are what bees create to store their eggs and larvae.

Cones:

A cone is a three-dimensional geometric shape that tapers smoothly from a flat, usually circular base to a point called the apex or vertex.

Volcanoes form cones, the steepness and height of which depends on the runniness (viscosity) of the lava. Fast, runny lava forms flatter cones; thick, viscous lava forms steep-sided cones.

Few more cones in nature:

Parallel lines:

In mathematics, parallel lines stretch to infinity, neither converging nor diverging.

These parallel dunes in the Australian desert aren't perfect - the physical world rarely is.

Fibonacci spiral:

If you construct a series of squares with lengths equal to the Fibonacci numbers (1,1,2,3,5, etc) and trace a line through the diagonals of each square, it forms a Fibonacci spiral.

Many examples of the Fibonacci spiral can be seen in nature, including in the chambers of a nautilus shell.