Locus
The set of all points that share a property. This usually results in a curve or surface. Example: A Circle is "the locus of points on a plane that are a certain distance from a central point". As shown below, just a few points start to look like a circle, but if you collect ALL the points, you will actually have a circle.

Basic

What is an Equation

An equation says that two things are equal. It will have an equals sign "=" like this:

x

+

2

=

6

That equations says: what is on the left (x + 2) is equal to what is on the right (6)
So an equation is like a statement "this equals that"

Parts of an Equation

So people can talk about equations, there are names for different parts (better than saying "that thingy there"!)
Here we have an equation that says 4x-7 equals 5, and all its parts:

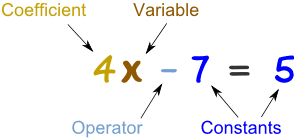	A Variable is a symbol for a number we don't know yet. It is usually a letter like x or y. A number on its own is called a Constant. A Coefficient is a number used to multiply a variable (4x means 4 times x, so 4 is a coefficient) An Operator is a symbol (such as +, ×, etc) that represents an operation (ie you want to do something with the values).
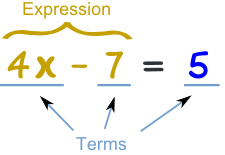	A Term is either a single number or a variable, or numbers and variables multiplied together. An Expression is a group of terms (the terms are separated by + or - signs)

So, now we can say things like "that expression has only two terms", or "the second term is a constant", or even "are you sure the coefficient is really 4?"

Exponents

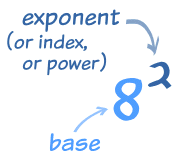The exponent (such as the 2 in x2) says how many times to use the value in a multiplication. Examples: 82 = 8 × 8 = 64 y3 = y × y × y y2z = y × y × z

Exponents make it easier to write and use many multiplications

Example: y⁴z² is easier than y × y × y × y × z × z, or even yyyyzz

Polynomial

Example of a Polynomial: 3x² + x - 2

A polynomial can have constants, variables and the exponents 0,1,2,3,...
And they can be combined using addition, subtraction and multiplication, ... but not division!

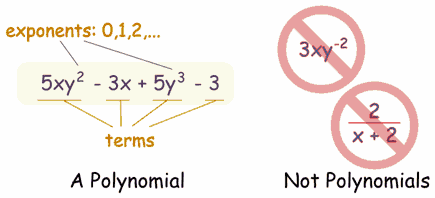
Monomial, Binomial, Trinomial

There are special names for polynomials with 1, 2 or 3 terms: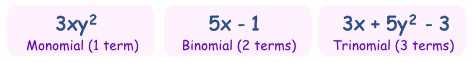

Like Terms

Like Terms are terms whose variables (and their exponents such as the 2 in x²) are the same.
In other words, terms that are "like" each other. (Note: the coefficients can be different)

Example:

(1/3)xy2

-2xy2

6xy2

Are all like terms because the variables are all xy²

Polynomial

Definition of a polynomial

Before giving you the definition of a polynomial, it is important to provide the definition of a monomial

Definition of a monomial:

A monomial is a variable, a real number, or a multiplication of one or more variables and a real number with whole-number exponents

Examples of monomials and non-monomials

Monomials	9	x	9x	6xy	0.60x4y
Not monomials	y - 6	x-1 or 1/x	√(x) or x1/2	6 + x	a/x

Polynomial definition:

A polynomial is a monomial or the sum or difference of monomials. Each monomial is called a term of the poynomial

Important!:Terms are seperated by addition signs and subtraction signs, but never by multiplication signs

A polynomial with one term is called a monomial

A polynomial with two terms is called a binomial

A polynomial with three terms is called a trinomial


Examples of polynomials:

Polynomial	Number of terms	Some examples
Monomial	1	2, x, 5x3
Binomial	2	2x + 5, x2 - x, x - 5
Trinomial	3	x2 + 5x + 6, x5 - 3x + 8

Difference between a monomial and a polynomial:

A polynomial may have more than one variable.

For example, x + y and x² + 5y + 6 are still polynomials although they have two different variables x and y

By the same token, a monomial can have more than one variable. For example, 2 × x × y × z is a monomial



Exercices

For all expressions below, look for all expressions that are polynomials.

For those that are polynomials, state whether the polynomial is a monomial, a binomial, or a trinomial

1) 3.4 + 3.4x

2) z² + 5z^-1 + 6

3) -8

4) 2c² + 5b + 6

5) 14 + x

6) 5x - 2^-1

7) 4 b² - 2 b^-2

8) f² + 5f + 6

Answer: 1), 3), 4), 5), 6), and 8) are polynomials. 1), 5), and 6) are binomials. 3) is a monomial. 4) and 8) are trinomials

2) and 7) are not because they have negative exponents

Notice that 6) is still a polynomial although it has a negative exponent. It is because it is the exponent of a real number, not a variable

In fact, 5x - 2^-1 = 5x + 1/2 = 5x + 0.5

It is subtle, but if you have any questions about the definition of a polynomial, feel free to contact me